H. Ahmadi, H.A. Rasheed
Abstract
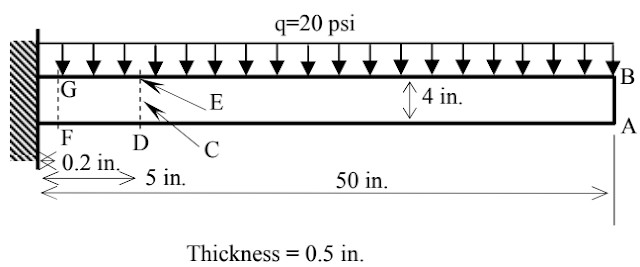
In this paper, a generalized semi-analytical approach for lateral-torsional buckling of simply supported anisotropic, thin-walled, rectangular cross-section beams under concentrated load at mid-span/mid-height was developed using the classical laminated plate theory as a basis for the constitutive equations. A closed form buckling expression was derived in terms of the lateral, torsional and coupling stiffness coefficients of the overall composite. These coefficients were obtained through dimensional reduction by static condensation of the general 6x6 constitutive matrix mapped into an effective 2 × 2 coupled weak axis bending-twisting relationship. The resulting two coupled stability differential equations are manipulated to yield a single governing differential equation in terms of the twisting angle. This differential equation with variable coefficients, subjected to applicable boundary conditions, was solved numerically using Mathematica. The resulting solution was found to correlate with the effective lateral-flexure, torsional and coupling stiffness coefficients to yield a general semi-analytical solution. An analytical formula was possible to extract, which was verified against finite element buckling solutions using ABAQUS for a wide range of lamination orientations showing excellent accuracy. The stability of the beam under different geometric and material parameters, like length/height ratio, layer thickness, and ply orientation, was investigated
A personalized link to the article